Love Triangle
Rating
8/10 You gotta love Matt Parker! And Jesi for borrowing me this book - thanks pal!
This book was a super enjoyable read and I bet anyone with a slight affection for math and a serious curiosity problem will enjoy it as much as I did. It’s funny, albeit full of dad-jokes that have about a 50% probability of landing where they intended to. Nonetheless, given the density of the jokes, there will be a passage during which you’ll giggle. It’s filled with fun facts, some of which I compiled in my notes, and it’s filled with a bunch of fascinating applications that just make you appreciate the human ingenuity and skill.
There were a few passages where I felt like the level of explanation is a little too trivial and it got me wondering about the right level at which a book like this should be written. I struggled with the same questions when creating some of my YouTube videos and I believe explaining such that my mom would understand is not the right way to go about this. The title and description of a book like this already does the pre-selection for who will actually read it - my mom would never pick this up. And as much as the goal can be: making math more widely accessible, one will only peak the interest of those who have been already a little interested in the first place. Thus, in my opinion, the book could have been written at a slightly higher level, being a little more technical, and not overly apprehensive about potentially boring details. Repetition is good, even necessary, as it helps you recall long-forgotten information, but ending an explanation of a fascinating theory or triangle application right before you get into the juice details simply feels like something was unnecessarily censored for those who would actually never read this book in the first place.
With that said, there were only a handful of instances where I thought of this, so 8/10 is my final verdict!
Synopsis
A book about a nerd’s love for triangles. Triangles here, triangles there, triangles everywhere. But you don’t have to love triangles to enjoy it - it’s non-triangle nerds friendly. You’ll love triangles by the end of it though. So read with caution.
Notes
- we have a super well preserved papyrus from roughly 1550 BCE that shows a sample of Egyptian mathematics - including some triangles!
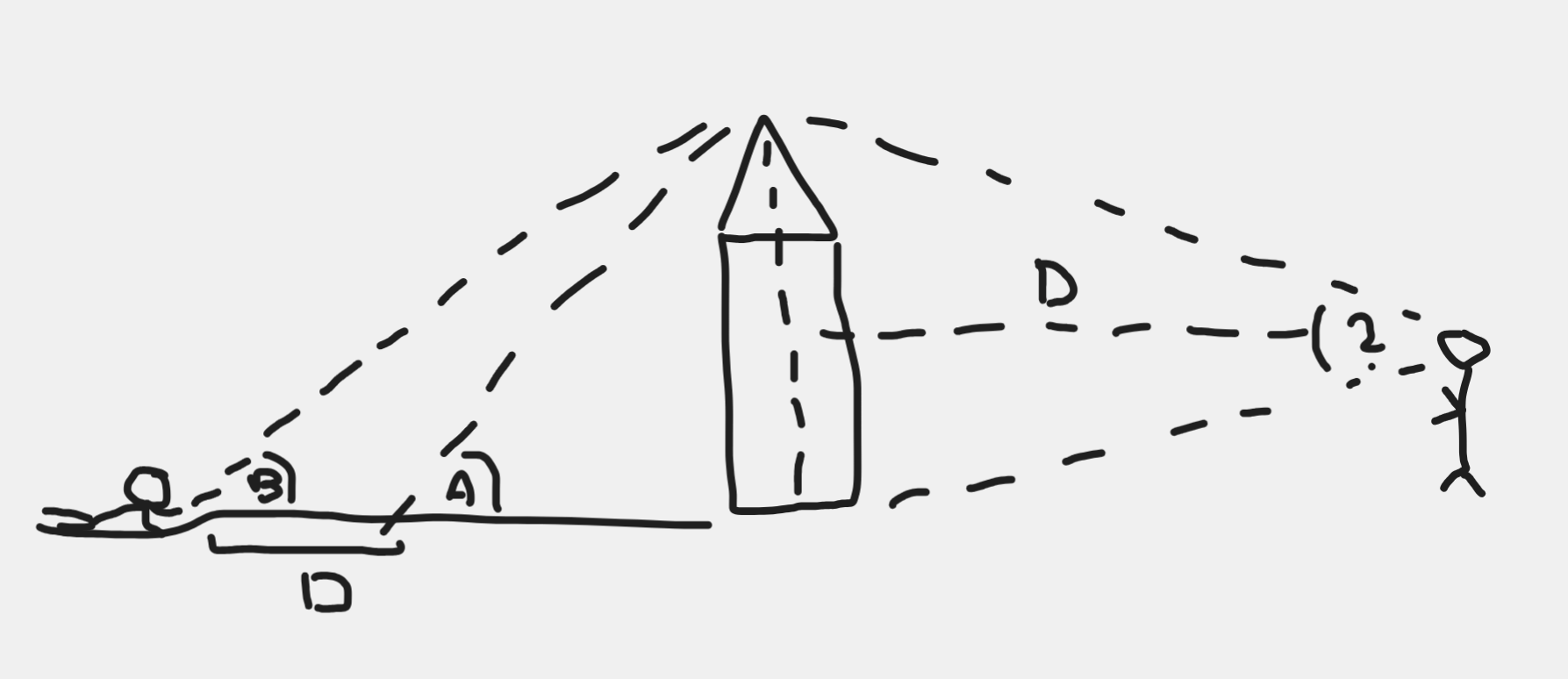
- if you know how far you are from an object you can measure it’s size with a protractor only! You find the angle between the top and the bottom edge of that object and then use some trigonometry to measure the triangles this arrangement creates
- or you measure the angle to the top of an object from one spot, then walk a certain known distance further, measure the angle again and another bunch of triangles is created with which you can measure the object’s height
- Hubble constant is a conversion factor that allows us to convert from red shift values (how much redder something looks like to us than it should be because of the expansion of the universe) and distance in kilometers (or miles or astronomical units if you can’t help yourself)
- we calculated the Hubble constant by using bunch of objects for which we knew both their distance from Earth and their red shift factor (I don’t really (yet) know how we could have known both - so further reading note)
- The value of Hubble constant is estimated to be between 67-74 $\frac{km}{\frac{s}{Mpc}}$ - that’s 67-74 kilometers per second per megaparsec
- mega parsec is 1 million parsecs which is approx. 3.26 light-years
- so Hubble constant/tension tells us that for every 3.26 light-years away from us any object is moving further away from us by 67-74km/s faster
- which is honestly such insanely tiny number compared to inter-galactic distances that it’s wild we managed to calculate this and it actually confirms with our observations
- From NASA: “For the first time, a spacecraft has sent back pictures of the sky from so far away that some stars appear to be in different positions than we’d see from Earth.”
- the definition of one meter is completely wild! As Europeans we have been making fun of Americans and British for using the imperial system but discovering the definition of meter I am starting to understand why we are possibly the weird ones here
- a meter has been originally defined as 1/10,000,000 (one ten-millionth) of the distance from the North Pole to the Equator. At the time we didn’t know what this distance was, so between 1792 and 1799 a bunch of French dudes measured a bunch of massive triangles over the European continent just so they can use some trigonometry to calculate this distance. Then they divided it by 10 million and voilà - a meter was born!
- Then, according to Wikipedia, in 2019 we decided this definition is not good enough (duh, since then we discovered that the French dudes were not as precise as they hoped for; albeit really close) so we redefined it as the length of the path travelled by light in vacuum during a time interval of 1/299792458 of a second, where the second is defined by a hyperfine transition frequency of caesium.”
- … and we say inches, ounces and miles are weird. Right.
- if you take some material, e.g. sand or glass or cement, and you simply pour it onto a straight surface, it will create a pile. The slope of this pile has a certain angle and as humanity we figured out that this angle is determined by the inherent friction coefficient of the material’s particles. That is, we can look at any pile of stuff, measure the angle of the slope and narrow down what kind of particles make up this pile - pretty cool!
- to calculate the area of a triangle, one usually needs to measure one of the heights. But what if that’s impossible or unpractical? Heron’s formula comes to rescue!
- Define $s=\frac{1}{2}(a+b+c)$ where $a$, $b$ and $c$ are the sides of a triangle
- Then $A=\sqrt{s(s-a)(s-b)(s-c)}$
- What the hell?
- What’s the most optimal division of the plane such that each individual tile has the smallest diameter? The answer is hexagonal/honeycomb division which was long believed to be the answer but only proven in 1999.
- What’s the equivalent of this but in 3D? The best space filling division with the smallest area between individual cells? The answer turns out to be an alternating arrangement of irregular dodecahedrons and tetrakaidecahedrons known as Weaire-Phelan structure
- In 2023 we finally discovered an aperiodic monotile - a single tiling shape that fills the plane without ever repeating a section. It was a worldwide sensation, but it is less known that few months later we actually proved that the tile comes from a continues family of hat tiles that all aperiodically fill the plane - can’t wait to tile my future bathroom :)
- being the nerd I am, one day I would love to make all of the Archimedean solids out of wood and glass
- Or make a big greenhouse in a shape of something like truncated icosidodecahedron
- I actually always wondered what do the road signs about hill steepness mean by the percentage that they state. Turns out the percentage is the ratio by which the height of the road changes over its length - aka rise over run, aka the slope. So actually the road signs show the tangents of the slope of the hill! Hence, if you want to get the actual slope, just arctan the shown percentage. You’ll be surprised how steep or rather non-steep a 10% or 15% hill really is.
- cosine rule is Pythagorean sentence but for any triangle, not just the right-angled ones
- we are all using GPS like it’s no biggie but we are at the same time literally employing the equations of special and general relativity to adjust for the time dilation that the satellites in orbit experience due to their high speed and lower gravity - so next time someone ask “bUt WhATs tHe acTUaL uSe CasE fOR rELatIVitY?” just disable their GPS signal :)
- also it’s pretty cool how we dealt with it - we simply sped up the ticking speed of the clocks in these satellites when manufacturing them - as easy as that. Except it wasn’t so easy to figure out by how much they had to be sped up. Imagine not having discovered general and special relativity, sending the satellites to space and then being surprised why the error keeps accumulating - I suppose we would come up with some kind of satellite constant :)
- gravitational waves are created by large objects moving through space or slamming into each other - objects like black holes or entire galaxies - we hypothesized that they exist but we never detected them until 2015
- in 2015 we detected a tiny tiny ripple in spacetime
- it literally moved our entire earth by less than an atom’s width, but we detected it! Isn’t science amazing?!
- we managed to detect (and hopefully correctly) attribute this tiny 0.2s long signal to an event that happened about 1.4 billion years ago when two giant black holes slammed into each other and release energy that’s about 50 times the energy of all stars in the universe today. That signal traveled to us for 1.4 billion years at the speed of light and on the 14th of September 2015 it moved the Earth by about an atom - and we managed to detect it. That’s so bonkers! I love science and I hate that we as humanity are destroying the planet, fighting wars and making life difficult for ourselves - instead of all being scientists and figuring out the wonders of this world, on Eartha and far far beyond it.