Probability of Improvement
What is this post about?
In this post I review the paper by Bouthillier et. al., where Bouthillier and his colleagues look into the degree of variance that exists in machine learning algorithm benchmarking. Somewhat unsurprisingly they found out that the variance is large and they provide a computationally managable way for more robust comparison of newly proposed deep learning algorithms.
The State-of-the-Art Problem
It’s a standard to compare deep learning algorithms based on their performance (eg. classification accuracy) on benchmark datasets such as CIFAR-10 or GLUE. In a worse case scenario, only a single model generated form a single training round of the proposed algorithm is considered. After that, it’s deemed State-of-the-Art (SotA) if it achieved the required $\Delta$ (delta) marginal improvement in its performance on the benchmark. In a better case scenario, the algorithm is trained multiple times with different data splits, hyperparameter values, data orders, weight initializations - aka sources of variance, after which the average model performance is calculated and deemed SotA if this average performance is better by the $\Delta$ margin. This is the better case scenario, since the comparison is more robust, thanks to, in some sense, accounting for variance that arrises from the training process. However, since machine learning is just a branch of statistics, this is still a rather weak way to compare different algorithms in this field. Generating a large sample with models that randomize all sources of variance and performing a t-test would be much more desirable. However, due to the growing size of the deep learning algorithms this is becoming computationally unfeasible (limited time and resources). Therefore, we cannot rely on CLT (central limit theorem) and t-tests and must come up with some alternative comparison methods.
The Probability of Improvement is one such potential method introduced by Bouthillier et. al. in their recent paper titled Accounting for Variance in Machine Learning Benchmarks. It offers a comparison method based on a non-parametric percentile bootstrapping for the variance estimation in order to overcome the computational limits of re-training huge networks many tens/hundreds of times. But before diving deeper into its crux, let’s first summarize their findings about the variance in the performance of the deep learning algorithms.
Sources of Variance
In the name of science, Bouthillier et. al. invested the resources into re-training several of the current SotA algorithms in order to measure their performance and quantify the degree of variance coming from the following sources:
| Hyperparameter Optimization | Learning Procedure |
|---|---|
| Random search | Data sampling (bootstrapping) |
| Grid search | Data augmentation |
| Bayesian optimization | Data visit order in gradient descent |
| Weights initialization | |
| Dropout |
What they found, after ~8 GPU years of computation on Tesla V100-SXM2-16GB, is that in nearly all of their case studies, each one of the above sources was a sizeable variance contributor except for dropout and data augmentation. Especially “problematic” were all three types of hyperparameter optimization, data sampling and weights initialization. These finidings are quite worrying, since due to the high computational costs of especially hyperparameter optimization, in most ML pipelines this is a one-and-done process. Moreover, the total size of the variance wasn’t negligible compared to the commonly used $\Delta$’s for performance comparison, showing that some of the crowned SotA’s may have not actually been SotAs at all, due to overlapping confidence bounds of their performance.
So in a nutshell, the case studies revealed that the variance in the performance of different algorithms is rather large and often unaccounted for. This in turn means that the amazing performance that your algorithm showed may be by a large part attributed to the randomness in the training procedure, instead of the claimed ingenuity of your ML pipeline. Cue the sad music…
Saving on Computation
So variance is quite a problem, but accounting for it is as well. What do we do? Well, how about fixing the most computationally costly sources, randomizing the rest and figuring out what happens to the variance? Sounds pretty good, thus it’s exactly what Bouthillier et. al. propose to do. More specifically, they propose to optimize the hyperparameters only once and randomize the other sources of variance to obtain a small sample of semi-randomized models. In such a procedure, the performance is conditional on the values of the optimized hyperparameters, therefore the variance estimator is biased, and the bias depends on the degree of correlation between the different “random” models - “random” in a sense that some partial sources of variance in the training procedure have been randomized. The more randomization, the less correlation, the more stable (lower standard error) of our variance estimator. To make this a little clearer, let’s borrow the notation and the definition of the variance estimator from the paper.
where $\tilde{\mu}_{(k)}$ is the biased performance estimator, $\hat{R}_e$ is the performance/Risk measure in our semi-randomized sample of models, $\rho$ is the average correlation between these models and $\xi$ is the conditioning variable that encapsulates the fixed sources of randomness, namely the hyperparameter pre-optimization. Now even more clearly the goal is to minimize $\rho$, which is achieved when as many sources of randomness are actually randomized. Otherwise the second term inflates the estimator, especially in small samples which are usually the case in the ML field - again, think computational costs are high.
Probability of Improvement
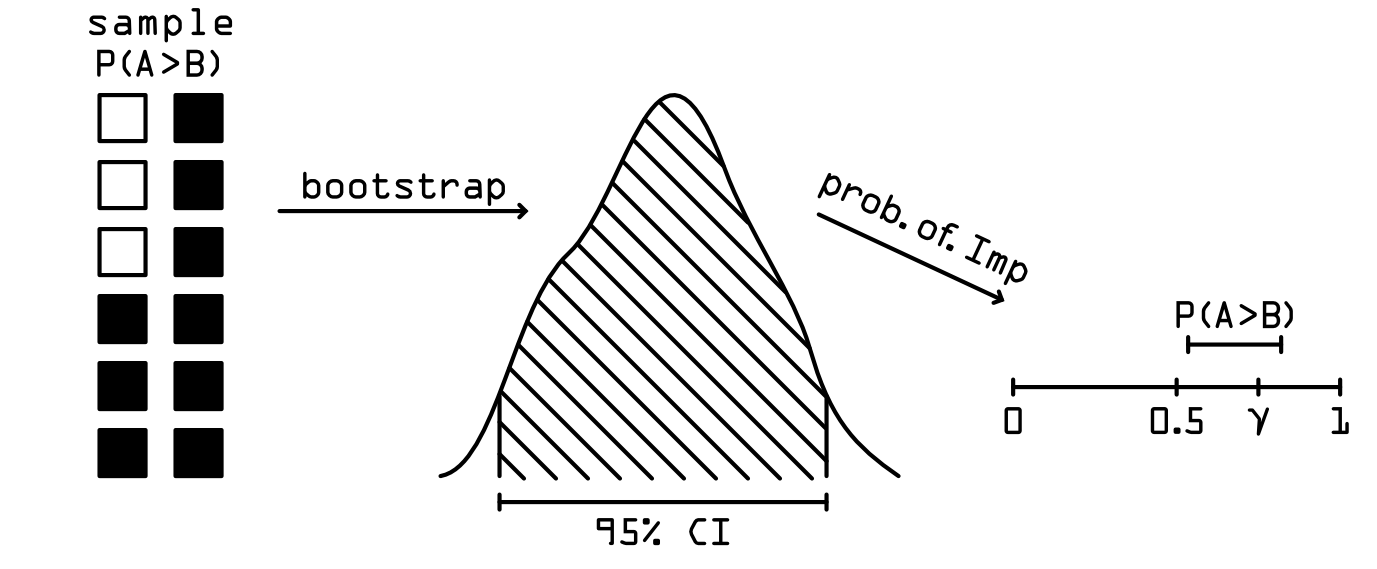
So finally we come to the Probability of Improvement, which is Bouthillier et. al.’s proposed way of robustly comparing ML models with the knowledge that due to the limited time and computation, their performance estimators, mean and variance, are most likely biased. The probability of improvement can be used when we train two algorithms, $A$ and $B$, on the same dataset with seeded randomized sources of variance and pre-optimized hyperparameters. Then, we can define \(P(A>B) = \frac{1}{k}\sum_{i=1}^kI(\hat{R}_{ei}^A > \hat{R}_{ei}^B)\), which is the proportion of times that the model $A$ outperformed the model $B$. In order to calculate the confidence bounds for $P(A>B)$ we take our sample of paired models and perform bootstraping with replacement, each time calculating $\hat{P}(A>B)$. This gives us a boostrapped distribution of $P(A>B)$ from which we can non-parametrically deduce the 95% confidence interval as the data between the 2.5-th and 97.5-th quantiles. From there we define two hypotheses:
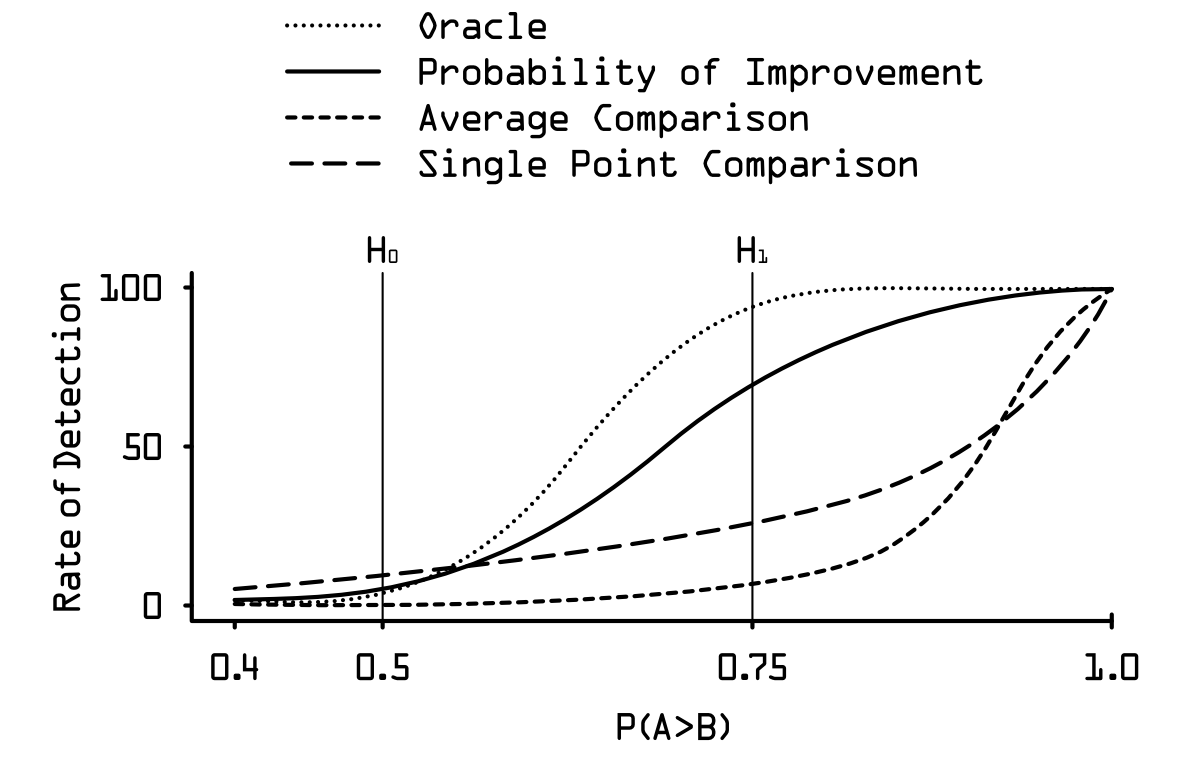
\[H_0: \: P(A>B) = 0.5\] \[H_1: \: P(A>B) = \gamma,\]where $H_0$ hypothesizes a statistically significant result, while $H_1$ hypothesizes statistically meaningful result. What we are after is both statistically significant and statistically meaningful outperformance of model $A$ on model $B$. That is, probability of outperformance concludes that $A$ is better than $B$, if and only if the lower bound of the confidence interval $P(A>B)$ is above 0.5 AND the upper bound is above $\gamma$. The visualization below summarizes this concept.
So What?
So why is this concept better than the comparison of the average performances of the models $A$ and $B$ ? Below I approximatelly reproduced the figure from the original paper that best illustrates the power of the probability of improvement. What you can see there is the comparison of all four methods: probability of improvement, average performance comparison, single-point comparison and an oracle that would be achieved using a t-test comparison. The x-axis denotes the proportion of times that the model $A$ outperformed model $B$, and the y-axis denotes the rate of detection of this outperformance. The higher the $P(A>B)$, the more certain we are about $A$, in fact, being better than $B$, thus the higher the rate of detection we want from our comparison method.
As you can see, the single-point and the average comparison methods are pretty bad in this respect. They are both highly conservative, which at first could be seen as a good feature, however, it is not! Imagine some paper comes out claiming their new algorithm is SotA based on the average comparison of its performances. They publish their code so everyhting is highly reproducable. People go, reproduce it and the majority of them finds out that in their replication, $A$ is actually not better than $B$. Then, this majority would claim that the original paper was just a false positive, and the new algorithm $A$ is in fact not SotA. However, the truth would be that $A$ is SotA, and just because the average comparison was used, the majority of replications got results that were false negatives, due to the biased nature of the performance metric in use.
Precisely for this reason, probability of improvement is a major update for the comparison methods between machine learning models, since it offers a proportion of false negatives and a proportion false positives that are much closer to the t-test which would be the ideal comparison method.